WebGL on Elm Architectureでmeshを変形させるお作法
WebGL世界におけるmesh変形とカメラとShaderを整理する。
勘違い
Three.jsに甘えたWebGL利用しかしてこなかったせいか、WebGLという概念への根本的な理解が色々と足りていなかった。
まずはmeshという概念。基本的にmeshは三角形ポリゴンの集合によって表現される。ここまでは問題ない。問題だったのはmeshを移動・回転させるお作法。
解説用meshを自前で用意するのは非常に手間なのでこちらのThree.js製Webエディターに全力で頼っていく。 https://threejs.org/editor/
とりあえず何の変哲もないただの立方体にご登場いただく。
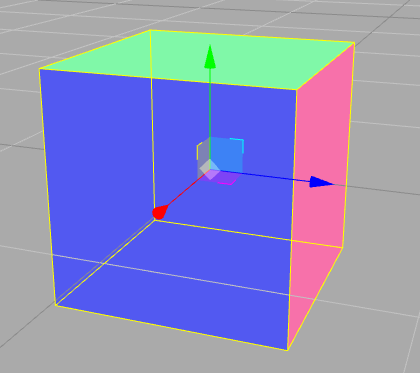
次にこの立方体を回転させたいと考える。

WebGLの気持ちをよく分かっていなった当初は、meshを回転させるには単純に「meshを構成する頂点をそれぞれ移動すればよい」とスーパーシンプルに考えてしまっていた。
もちろんこの方法でもmeshは回転した状態でWebGLは描画してくれる。しかしながらこのときの「回転した状態」というのは大きな語弊がある。正確に表現するなら、「元のmeshの頂点をそれぞれ回転させた頂点から新たに生成したmeshに差し替えた状態」である。要するに回転させる前と後のmeshは全く別の存在になってしまっている。
mesh生成コスト
meshの生成には常にコストという問題が付き纏う。WebGLは確かに高速な3D描画機能を提供してくれる。しかし描画するためのmeshを生成するのはWebGLではなくスクリプト側である。
一度の回転だけならまだしも回転アニメーションを作ろうとすれば、毎フレームmeshを回転させなければいけない。もしmesh差し替え方式で回転を表現したら、毎フレームmeshの新規作成が行われるという贅沢すぎる状況となってしまう。
3D描画のパフォーマンス劣化を防ぐためにも、まず第一にmesh生成を最小限に抑える必要がある。
カメラを動かす
mesh自体の頂点を回転させる方法がだめならどうやって回転を実現するか。meshが動かないならカメラを動かせばよい。
カメラを動かすとこうなる。
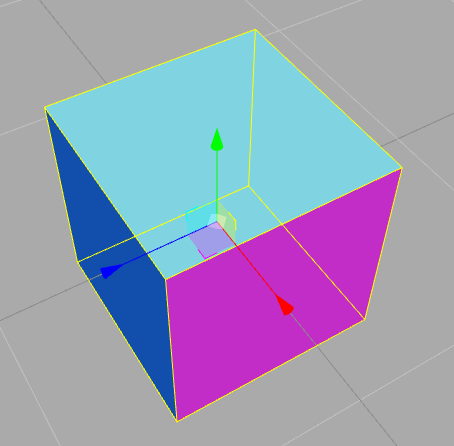
meshは見事に回転した状態で描画された。そしてmesh自体は元のままなので再生成も行われていない。パフォーマンス劣化もない。めでたしめでたし。
当然ながら物事はそんなにシンプルではない。だってカメラ自体をを回転させたら3D空間全体が回転してしまうではないか。背景も何もない空間にただ1つのmeshを登場させるだけでいい状況でしか使えない方法ではないかというツッコミが溢れる。
しかしその考え自体が既にThree.js概念に引きずられていて、WebGL的概念に辿り着けていない。
前回記事 でも触れたように、WebGLの世界に「カメラ」という概念は存在しない。
WebGLとカメラ
WebGLの世界にカメラが存在していないのなら、3D空間を平面に描画しているこの視点の位置は一体なんなんだという疑問が当然出てくる。
結論から言うとそれはカメラではない。単にその位置から見えているように、それぞれのmeshを変形させた平面像をcanvasに描画しているに過ぎない。
この変形という役割を担っているのがShaderである。任意のmeshには任意のShaderによる変形を加えることができ、WebGLは変形後の3D表現をただの平面へと描画する。
イメージとしては以下のような流れ。mesh毎にshaderが適用でき、同じshaderを使わなければならないといった制限は特にない。
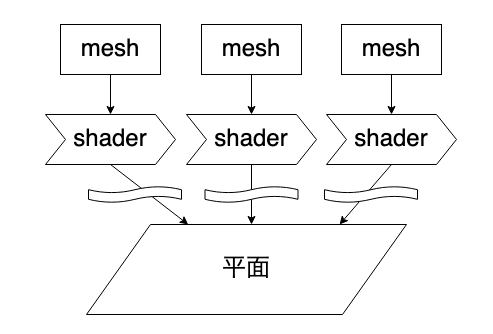
謎のニョロニョロで誤魔化しているように実際には平面に辿り着くまでもう少し要素がある。今回の話題との関連は薄いので省略御免。
ちなみにこの変形を行うShaderのことを、「頂点シェーダ」「vertex shader」と呼ぶらしい。実際は他にもShaderは存在するが、簡略化のために記事内でのShaderは全てこの頂点シェーダのことを指しているものとする。
ElmのWebGLサンプルでもそのような名称のShader実装を用意してくれている。
ShaderはGLSLというJavaScriptでもElmでもないWebGL制御用言語で記述される。突然の新言語登場に面食らいやすいが、実はやっていることはmeshの格頂点に対するただの座標変換だけだったりする。GPUで計算してくれそうな気配があるので、おそらくスクリプト側で行列計算するよりも高速なのではないだろうか、詳細は未確認。
gl_Position = matrix * vec4(position, 1.0);
Shaderの正体がただの線形代数的な座標変換ということが分かったので、例えば変換行列をこんな風に表現することも可能なのである。
gl_Position = camera * transform * vec4(position, 1.0);
matrixという4次元行列を同じく4次元行列のcameraとtransformの積で表している。行列の掛け算なのでもちろん順番には注意が必要。
式だけ見たらmatrix = camera * transformな恒等式ではないかと思ってしまうが、この分解がWebGLというレンダリングエンジンを人間に理解できる3D世界表現に翻訳するための大きな助けとなってくれる。
文字通りこのcameraという行列が3D空間における我々の視点であるカメラとなる。そしてtransformによって、それぞれのmeshに自由な変形を施すことも可能となっている。
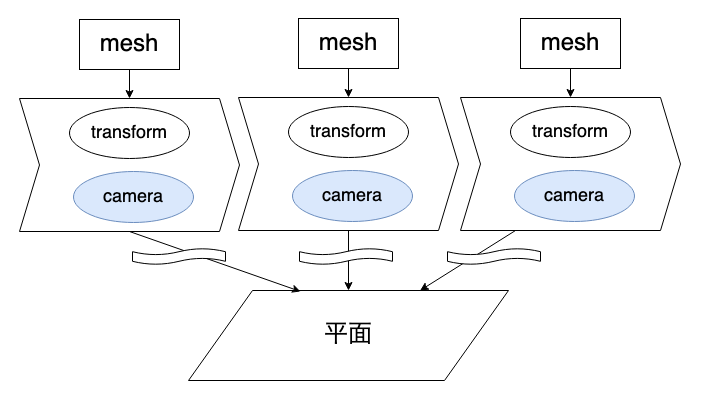
カメラとmesh変形
mesh自体の頂点を回転させる方法がだめならどうやって回転を実現するか。meshが動かないならカメラを動かせばよい。
mesh変形方法に関してのこの記述も、どういうことなのかもう察しがついてきているはず。結局ところShaderが行うのは変換行列によるただの座標変換なのだから、その行列を分割して、「視点となるグローバルなカメラ」と「個別meshの変形を行うための専用カメラ」をそれぞれ用意することができるのである。
描画までの流れは次のようになる。
- それぞれのmeshに対する変換行列(
transform)による座標変換を行う - 全てのmeshで共通の変換行列(
camera)による座標変換を行う - レンダリングエンジンに引き渡す
Elm
WebGLサンプルにShader実装も載っているが、単一のmeshしか存在しない世界を想定しているような実装になっていてそのままだとやや使いにくい。
視点用カメラとmesh変形を分けて扱うために調整するとこのような雰囲気。カメラやmesh変形をどういうデータ構造でModelに持つかによってShader側も自前で調整していくといいかもしれない。
type alias Uniforms =
{ transform : Mat4
, perspective : Mat4
, camera : Mat4
, shade : Float
}
vertexShader : Shader Vertex Uniforms { vcolor : Vec3 }
vertexShader =
[glsl|
attribute vec3 position;
attribute vec3 color;
uniform mat4 perspective;
uniform mat4 camera;
uniform mat4 transform;
varying vec3 vcolor;
void main () {
gl_Position = perspective * camera * transform * vec4(position, 1.0);
vcolor = color;
}
|]
ElmというよりほぼWebGL自体の話題だったが今回のまとめはここまで。